[The preliminary results herewith reported are part of a currently ongoing research]
|
Glimpse |
|
| The movement of an observer in a structured environment leads to a specific retinal optic flow with a strong expansion component. Let's immagine that such motion stimulus be (qualitatively) represented by another motion pattern characterized by radially expanding traveling waves. Assuming a complex-log mapping, radially expanding traveling waves are mapped into right-ward traveling waves. On a purely speculative ground, we assume that these right-ward traveling waves approximate a phenomenological cortical activation (``cortical flow'') in response to the original motion stimulus. Having adopted this representation, the analysis of the properties of the motion stimulus can be performed by spatiotemporal filtering operations on the ``cortical flow''. The results of these spatiotemporal filtering operations are considered as the responses of MST-like cells. | |
|
Preamble: |
|
|
In extrastriate areas the functional properties of cortical cells are
usually described in a parametric space: cells are stimulated by
velocity patterns and their activities give indications about their
sensitivity
to a specific motion stimulus characterized by a specific direction,
velocity,
global expansion/contraction, global rotation, etc. This description turns
out to be extremely effective to characterize the behavioural
properties
of cortical cells, but it does tell us nothing about how such cells gain
their functionalities (i.e., the neurophysiological basis of their
behaviour).
Moreover, such description in the parametric (i.e., velocity) space is
adequate for a theoretical investigation on the properties of optic flow
(Koenderink, 1986) in terms of vector calculus.
However, we believe that cortical cells do not know Green's theorems (cf.
Poggio et al., 1991; Verri et al., 1992; Zhang et al., 1993) and therefore
they cannot perform
vectorial operations. They only can do what they are engineered for: that
is, spatiotemporal integration.
On such motivations the idea of adopting an alternative representation of the optic flow compatible with the physiological properties of cortical cells. |
|
|
The Cortical Flow |
|
|
The basic assumption of our model starts from a speculation,
partially supported by experimental evidence that when a subject is
stimulated
by motion stimuli, ordered patterns of dynamic activations arise within
retinotopically organized visual areas.
In particular, we assume that a motion stimulus in the visual field activates
a dynamic pattern of activation
on a localized portion of cortical areas. This activation could be
intended
as a macroscopic (i.e, averaged) activity (cf. also neural field approach)
that can be compared to spatiotemporal flow of excitation revealed by
current
source density analysis, local field potentials, optical imaging, or, at
higher scales of observations by fMRI.
Given the retinotopic properties of visual areas (V1, MT) the
topographic
properties of the stimulus are preserved according to a complex-log mapping
(Schwartz, 1977) [cf.
recent studies by fMRI revealed that expanding ring stimuli
or rotating wedges stimuli (stimuli were composed of a contrast-reversing
checkerboard pattern flickering at 8Hz) create traveling waves of neural
activity within retinotopically organized visual areas ( Engel et al., 1997)].
Formally, to construct such cortical representation of a motion
stimulus,
we map the optic flow
More specifically, to each vector in the optic flow we associate a
localized
traveling wave (wavefront) moving along the cortical direction
corresponding
to the retinotopic mapping with a velocity proportional to the velocity
of the motion pattern:
The resulting flow of activation f(x,y,t) (hereafter referred as the ``cortical flow'') is the superposition (interference) pattern of all the localized wavefronts. |
|
|
MST cell modeling Each MST neuron is selective to an elementary flow component referred to the fixation point (i.e., the preferred center of motion of the cell is located on the fovea) and is characterized by a specific tuning to the mean speed of motion of optic flow stimuli. Thus, from a behavioural point of view, MST neurons act as weight vector fields performing a template matching of cell preferences over a portion of the optic flow stimuli. On the basis of the spatiotemporal representation of the optic flow (the cortical flow), and taking advantage of the geometrical properties of the log-polar mapping, the template vector matching operations can be reconducted to spatiotemporal filtering operators characterized by directionally-tuned kernels to detect translational motion of the cortical flow. The approach can be straightforwardly generalized to combinations of rotation and expansion/contraction, i.e., to spiral motions (Graziano et al. 1994), by considering filters oriented along oblique directions. Preliminary simulations showed that the characteristic features of our MST-like units, resulting as emergent properties of the geometrical organization of our model, resemble those observed in real cells. |
|
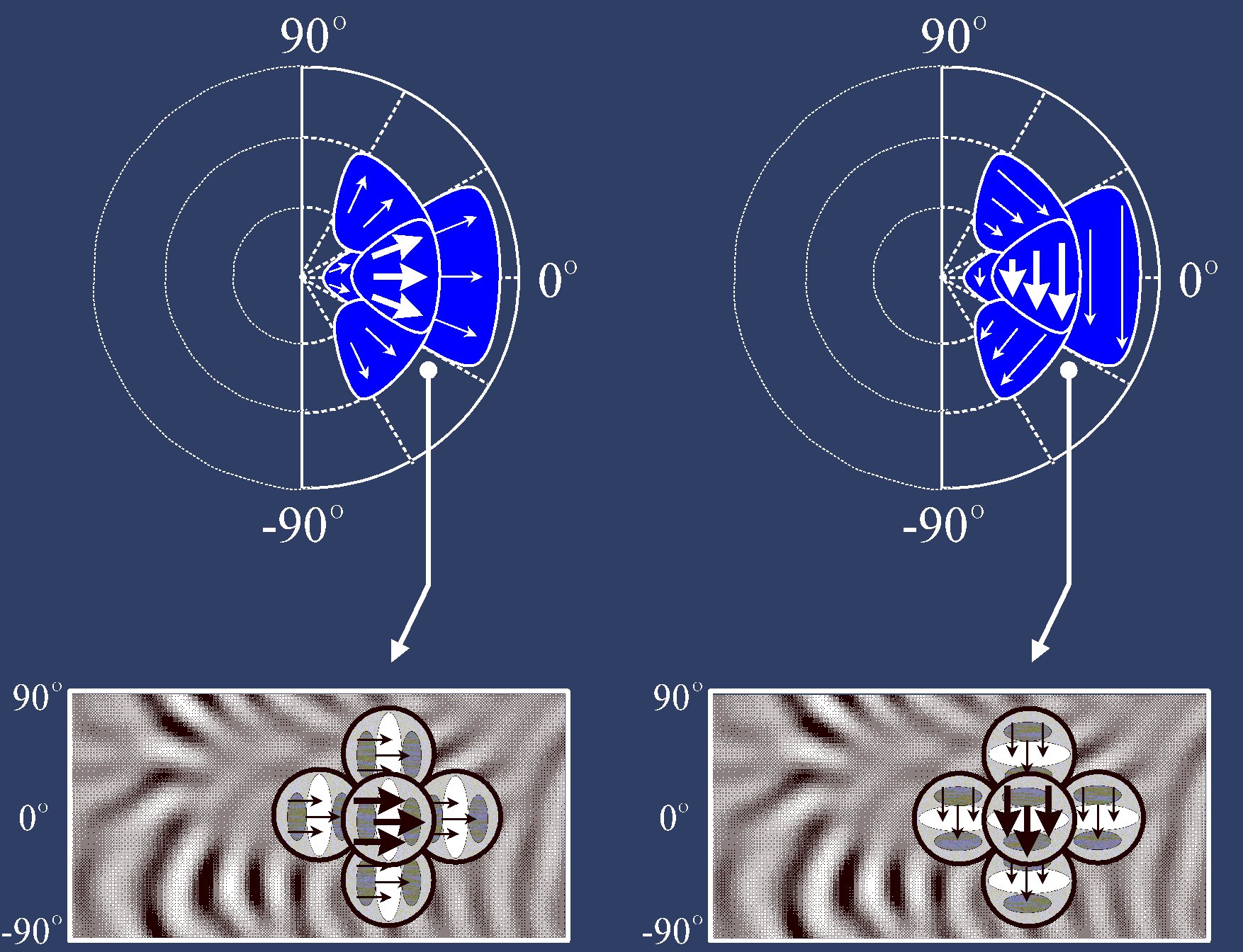
|
Conclusions and perspectives |
|
The primary property of our model is related to the introduction of a
physicalist (i.e., spatiotemporal) representation of the optic flow
which transforms the input vector field into a dynamic cortical activation
pattern (cortical
flow). In this way, MST cells' sensitivity to first-order differential
properties of the optic flow depends on their capability of detecting the
direction of cortical motion. This occurs through direct spatiotemporal
filtering operations on the cortical flow.
The model is similar to other template models (e.g., Perrone and Stone, 1998)
but it differs from them in two respects: our MST
cells are speed tuned, and the templates are made of portions of
elementary flow components always centered on the fovea.
Accordingly, for each model cell the best stimulus should be centered on
the
fixation point, though, different stimulus
configurations can trigger a cell response, provided that the sub-pattern
of
the optic flow locally matches the cell preferences for motion component
and speed.
In a hierarchical perspective, our MST cells can be considered as
basic units whose responses can be combined to obtain more powerful
descriptors characterized by larger field aggregate selectivity.
In this perspective, the role of lower-level MST neurons in interpreting optic flow
fields would be one of responding to visual motion according to the degree
of match between the visual input and the preferred optic flow field of the
neuron, whereas a qualitative analysis of the fundamental features of optic
flow (e.g., the detection of differential invariants) would be the role of
higher-level MST neurons.
These considerations suggest that the numerous, and sometimes contradictory
physiological cell properties relating MST cell response to the placement
of optic flow stimuli in the visual field, including position invariance,
center-of-motion tuning, direction reversals,
could be re-examined from this new (gaze-centered)
perspective.
The center-symmetric selectivity preference of MST units could be also related to an ``ecological'' requirement in connection with their capability of judging heading direction and time-to-collision. A direct consequence of the gaze-centered representation is, indeed, the observation of maximal distribution of activity on MST layer when the preferred component is centered on the fixation point. This emphasis on central vision may have important implications for visual navigation since the direction of motion would most likely be foveated. |
|
| Examples of optic flow representations obtained by our model can be seen here. | |